Working with the smoothing parameters

FastTrackPy smooths formant trajectories using a form of Discrete Cosine Transform. Here’s how you can convert the DCT parameters back into formant track smooths after, e.g. averaging them.

import polars as pl
import matplotlib.pyplot as plt
from scipy.fft import dct, idct
import numpy as np
from fasttrackpy import process_corpus
from pathlib import Path
corpus_path = Path("..","assets", "corpus")
measurements = process_corpus(corpus_path)
100%|██████████| 65/65 [00:01<00:00, 62.80it/s]
100%|██████████| 274/274 [00:01<00:00, 224.56it/s]

Let’s just look at /ay/ from these speakers.

ays = [track for track in measurements if track.label == "AY1"]
ays[0].winner.spectrogram()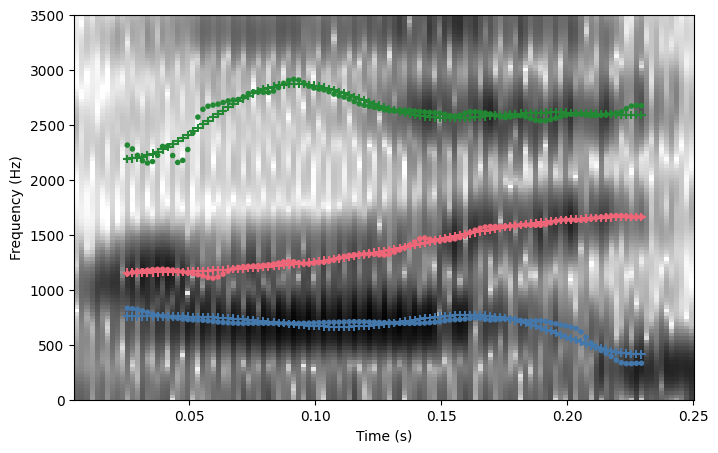

The Discrete Cosine Transform

The smoothed formants are a 5th order discrete cosine transform. The DCT parameters are estimated via regression, using the following basis.

time = ays[0].winner.time_domain
N = time.size
order = 5

full_basis = dct(
    np.eye(N), 
    orthogonalize=True, 
    norm = "backward"
)

basis = full_basis[:,:order]

plt.plot(time, basis)
plt.legend(range(5))
plt.show()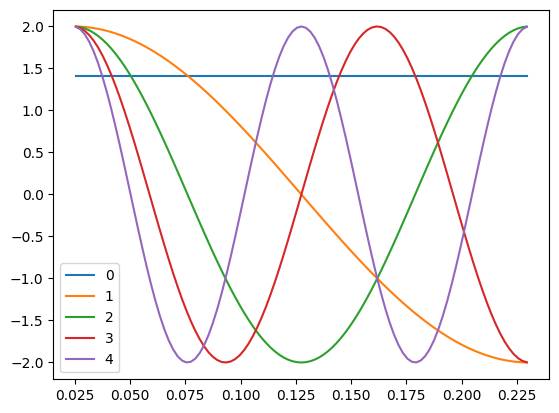

DCT coefficients define how to weight and sum this bank of cosine functions to match the input signal.

# the dct coefs for f1
f1_params = ays[0].winner.parameters[0,:]

# the formant track
f1 = ays[0].winner.formants[0,:]

plt.plot(time, basis * f1_params)
plt.title("weighted coefficients")
plt.show()

plt.plot(time, basis @ f1_params)
plt.plot(time, f1)
plt.title("weighted and summed")
plt.legend(["DCT", "F1"])
plt.show()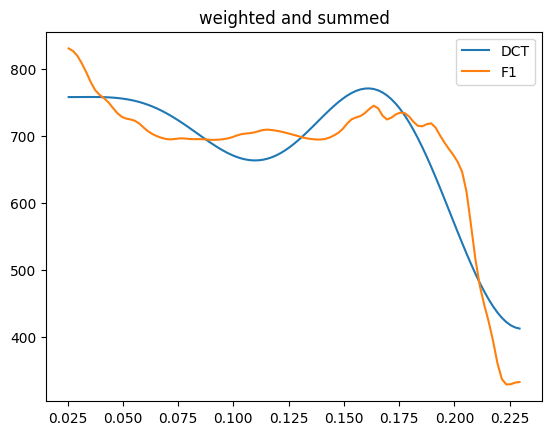

It’s possible to estimate DCT coefficients directly with scipy.fft.dct, but because there is potential for missing data in some formant tracks, FastTrackPy instead estimates the DCT coefficients using regression.

def reg_fit(x, basis):
    params = np.linalg.inv(basis.T @ basis) @ (basis.T @ x)
    return params

params = reg_fit(f1, basis)
print(params)
[480.35423508  42.95237019 -25.847216    43.60350087 -21.40266949]

Inverting the DCT

It’s possible to invert the DCT parameters with scipy.fft.idct(), with orthognalize = True and norm = "forward". You also need to define how large you want the resulting smooth to be with n

f1_smooth = idct(
    params, 
    n = time.size, 
    orthogonalize=True, 
    norm = "forward"
    )

plt.plot(time, f1_smooth)
plt.plot(time, f1)
plt.legend(["smooth", "F1"])
plt.show()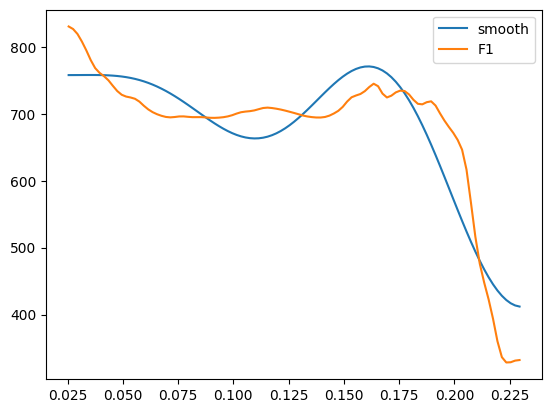

Benefits of using the DCT parameters

“Down sampling”

It’s somewhat commmon to reduce the number of measurement points from a formant track to a common number (e.g. 20 evenly spaced points). We can achieve that by inverting the DCT parameters and using differently sized outputs.

smooth_100 = idct(params, n = 100, orthogonalize=True, norm = "forward")
smooth_20 = idct(params, n = 20, orthogonalize=True, norm = "forward")

plt.scatter(
    np.arange(100)/99,
    smooth_100
)

plt.scatter(
    np.arange(20)/19,
    smooth_20
)
plt.legend(["100", "20"])
plt.show()

Averaging

Instead of point-wise averaging over formant tracks, you can instead average over the DCT parameters, then invert the average. We can get a polars data frame of all of the parameters of /ays/ from these speakers with the .to_df() method,

all_ay_param = pl.concat([
    ay.to_df(output = "param")
    for ay in ays
])
all_ay_param.head()
shape: (5, 10)
param F1 F2 F3 F4 error file_name id group label
u32 f64 f64 f64 f64 f64 str str str str
0 480.354235 979.982402 1844.645657 2375.309331 0.007663 "KY25A_1" "0-0-8-1" "KY25A" "AY1"
1 42.95237 -130.966974 -15.909405 2.074594 0.007663 "KY25A_1" "0-0-8-1" "KY25A" "AY1"
2 -25.847216 13.467448 -67.211033 -35.364144 0.007663 "KY25A_1" "0-0-8-1" "KY25A" "AY1"
3 43.603501 4.180242 -84.055828 18.796364 0.007663 "KY25A_1" "0-0-8-1" "KY25A" "AY1"
4 -21.402669 -2.113492 -42.2589 -20.556695 0.007663 "KY25A_1" "0-0-8-1" "KY25A" "AY1"

To get the the average of each parameter for each speaker, we need to group the dataframe by the param, file_name and group columns, then aggregate them.

ay_param_means = (all_ay_param
 .group_by(
     ["param", "file_name", "group", ], 
     maintain_order = True)
 .agg(
     pl.col("F1").mean()
 )
)
ay_param_means.head()
shape: (5, 4)
param file_name group F1
u32 str str f64
0 "KY25A_1" "KY25A" 509.370491
1 "KY25A_1" "KY25A" 44.866749
2 "KY25A_1" "KY25A" -8.803074
3 "KY25A_1" "KY25A" 27.038315
4 "KY25A_1" "KY25A" -11.637004

Here’s the fitted F1 for the first speaker.

speaker_params = ay_param_means["F1"][0:5]
speaker_fit = idct(
    speaker_params,
    n = 100,
    orthogonalize=True,
    norm="forward"
)

plt.plot(speaker_fit)
plt.show()

The code below for getting fitted F1 tracks for each speaker is a bit detailed with respect to how polars dataframes work, but the process could be replicated in whatever way a user feels comfortable.

ay_fits = (
    ay_param_means
    .group_by(["file_name", "group"])
    .agg(pl.col("F1"))
    .with_columns(
        f1_fit =pl.col("F1")
                  .map_elements(
                      lambda x: idct(x, n = 100, orthogonalize=True, norm = "forward").tolist(),
                      return_dtype=pl.List(pl.Float64)
                      ),
        time = pl.lit(np.linspace(0,1,100).tolist())
    )
    .explode(["f1_fit", "time"])
)
ay_fits.plot(
    "time",
    "f1_fit",
    by = "group"
)

Getting derivatives

If we wanted to get the first derivative (or the rate of change) of the formant track smooths, this can also be calculated (code modified from here.)

from scipy.fft import idst

def first_deriv(coefs, size = 100):
    hatu = coefs.copy()
    for i in range(hatu.size):
        hatu[i]=-(i)*hatu[i]
    hatu[:-1]=hatu[1:]
    hatu[-1]=0
    dotu=idst(hatu, n = size, type=2)
    return dotu
speaker_fit = (
    ay_fits
    .filter(pl.col("group").str.contains("group"))
)

speaker_params = (
    ay_param_means
    .filter(pl.col("group").str.contains("group"))
    .select("F1")
)

speaker_rate = first_deriv(speaker_params["F1"].to_numpy(), size = 100)
fig, axes = plt.subplots(nrows= 1, ncols=2)
axes[0].plot(speaker_fit["f1_fit"])
axes[0].set_title("f1")
axes[1].plot(speaker_rate)
axes[1].set_title("first derivative")
plt.show()